Présentation de la suite de logiciels mecaflux:
Modelisation helice aerienne dans heliciel Modelisation helice bateau dans heliciel Modelisation helice ventilation dans heliciel Modelisation helice eolienne dans heliciel Modelisation hydrolienne dans heliciel Modelisation helice kaplan dans heliciel
L'énergie disponible L'énergie que nous pourrons capter éoliennes turbines et hydroliennes turbines hydroélectriques
Le captage de l'énergie des courants de fluide avec un système d'hélice est rencontré dans de nombreux système de production d'énergie et de force motrice.

projet d'eoliennes integréesHydrolienneCaptage d'air chaud dessiné par Léonard de Vinciturbine hydroelectrique

Les caractéristiques du fluide capté, air ou eau, modifient certaines contraintes, mais le principe de conversion de l'énergie reste le même. Donc avant d'étudier plus en détails les eoliennes , hydroliennes , ou turbines hydroélectriques, nous allons faire le point sur cette méthode de conversion de l'énergie.

 

Avant de se lancer dans le dessin de l'hélice , il faut évaluer le besoin en énergie et le comparer à l'énergie disponible sur le site de l'implantation. L'énergie tirée du fluide est de l'énergie cinetique.L'énergie cinétique, c'est l'énergie de la vitesse d'un objet. La puissance c'est la quantité d'énergie par seconde .En 1 seconde la masse(kg) de fluide traversant l'hélice = volume(m3)fluide traversant le disque de l'hélice X masse volumique(kg/m3) = Le calcul de la puissance du fluide traversant une hélice est donc : Cette équation nous fait apparaître les acteurs de la puissance de notre hélice de captage et leur importance:
Nous remarquerons que la puissance est une fonction cubique de la vitesse et que le doublement de la vitesse multiplie la puissance par huit!
La surface du disque balayée par l'hélice est le meilleur indicateur de son potentiel.

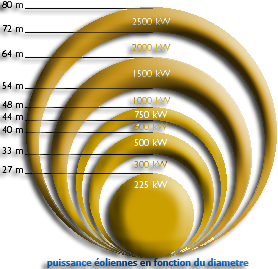
puissance eolienne en fonction diametre

 

L'énergie que nous pourrons capter:
Toute transformation d'énergie implique des pertes.
La première perte incontournable tient du fait que pour tirer toute la puissance de la vitesse du fluide, il faudrait lui enlever toute sa vitesse lorsqu'il traverse l'hélice. Tout le fluide qui entre dans l'hélice, si on l'arrete net, on le met ou? Il faut bien qu'il soit évacué de l' autre coté de l'hélice, et ceci suffisamment rapidement pour laisser de la place pour l'air arrivant ! Nous ne pourrons donc utiliser qu' une partie de la puissance du courant de fluide. Plus l'hélice enlève de vitesse au fluide, plus elle bouche le passage et plus le fluide perd son énergie sans la transmettre a notre hélice..
Pour une explication plus mathématique la théorie de froude utilisant la notion de quantité de mouvement peut être consultée.
Entre le cas ou l'on enlève aucune vitesse au fluide et le cas où l'on bouche le passage, il existe un cas où l'on extrait le maximum possible d'énergie du fluide. Ce cas idéal correspond à une diminution de la vitesse du fluide de 1/3 de sa vitesse en amont. Le maximum d'énergie récupérable (calculé et démontré par Betz) est de 16/27 de l'énergie du fluide. C'est la limite de Betz: Pour de l'air de masse volumique 1.25 kg/m3 ceci nous donne:
Pour de l'eau de masse volumique 1000 kg/m3 ceci nous donne:
  • equ5_B:Pmax(W)=296 X (surface disque hélice m²) X (vitesse eau m/sec)³
Le rendement d'une transformation d'énergie peut être évalué par: Puissance avant transformation / Puissance apres transformation . Notre hélice va transformer la puissance du fluide en une puissance sur l'arbre de l'hélice. La qualité de notre hélice sera révélée par son coefficient de puissance(Cp) calculé comme ceci:
Le Cp max théorique annoncé par Betz ne tient pas compte des pertes due au traînées et pertes en bout de pale des profils.En réalité ces pertes font que les meilleurs hélices ne dépassent pas les 70_80% de la limite de Betz. Ceci réduit notre Cp max espéré à 0.4_0.5
On trouvera donc rapidement la surface, donc la longueur de pale à donner à notre hélice pour nous fournir la puissance désirée si l'on connaît la vitesse du vent et que l'on estime le rendement(Cp) à 0.4: surface_disque_m2=longueur pale² x3.14 En partant d'un Cp optimiste de 0.4: Que se soit pour une éolienne ou une hydrolienne nous savons donc maintenant évaluer notre longueur de pale en fonction de l'énergie recherchée et de l'énergie du fluide. Nous allons maintenant nous intéresser à la combinaison de la vitesse de rotation et de la vitesse du fluide:Le point de fonctionnement de notre hélice

Petit intermède:

Est il possible de dépasser la limite de betz!...En empêchant le contournement de l'hélice grâce à un conduit entourant l'hélice, certain dispositifs semblent dépasser la limite de Betz, chiffres a l' appui! Mais cet artifice repousse le contournement (limite de Betz) au début du conduit! Le rendement de l'hélice (CP) c'est: Cp=puissance_arbre_hélice_w / (0.5 X masse_volumique_m3_kg X Vitesse_fluide_ms³ X surface_disque_m2). Si quelqu'un vient vous dire que le rendement de son système est supérieur à 0.59.., Vérifiez que la surface du disque corresponde à la surface réellement captée, et non à la surface balayée par l'hélice placée en bout de réduction du cône d'entrée! Un autre artifice consiste à aspirer le bouchon formé en arrière de l'hélice grâce à des anneaux profilés qui utilisent de l'énergie externe à la veine de fluide pour créer une dépression à l' arrière de l'helice.La surface réellement captée est là aussi modifiée! les meilleurs hélices ne dépassent pas les 70_80% de la limite de Betz, Ces systèmes carénés ont leur avantage car ils réduisent les pertes en bout de pale et augmentent le rendement de l'hélice, mais jamais au dessus de la limite de Betz! L' augmentation du rendement apporté par ces carénages doit être comparé au coût de fabrication supplémentaire, et là souvent, avec la matière ajoutée on pourrait augmenter le diamètre de l'hélice et la puissance globale du système!