Apparent velocity and apparent angle

The apparent speed, and apparent angle determine the twist of blade propellers

Understand and master the apparent velocity and apparent angle:

When a cyclist moves on a road 30 m / sec by a windless day, the relative velocity of wind for him to 30 m / sec. This bike can say that the apparent wind of 30 m / sec and it comes from the front. If the wind starts blowing facing him, the apparent wind speed will be composed of the speed of the cyclist and the wind speed.

If the wind blows perpendicularly with a speed of 1 m / sec, the apparent wind will be made primarily on the speed of the cyclist and will almost face
if perpendicular wind blowing at 30 m / sec, the apparent wind will all face perpendicular and that will be felt by the rider at 45 ° off course
If the wind starts to blow at 800 m / sec the rider feel the wind almost perpendicular to the road is 90 °. Note also that he risk of permanently stop the bike with such a wind...

For a propeller blade element located at radius r, the relative speed is composed of the peripheral speed (m / sec) and the velocity V of the fluid upstream of the propeller.

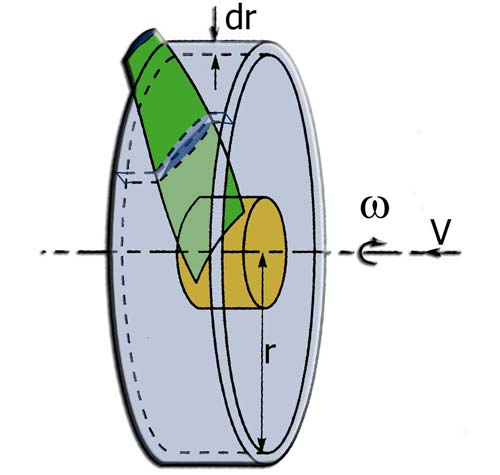
elements de pale et vent apparent

The peripheral speed Vp is related to the radius r and the rotation speed w (in rotation per second) as follows: Vp(m/sec)= w X 3.14 X r X 2 It is therefore more important at the blade tip that near the center....

The apparent angle received by a profile placed on radius r is thus the sum of the peripheral speed and the speed of the fluid upstream of the propeller:

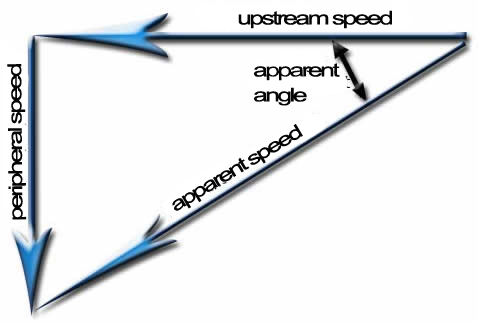
angle apparent et vitesse apparente

the apparent wind speed (m / sec) is therefore :

(pythagore)=sqrt(Vp²+V ²)

where Vp (m/sec) is the peripheral speed=( w X 3.14 X r X 2) and v is the speed of the fluid upstream (m/sec)

tangent(apparent angle)=Vp/V
The apparent angle is therefore = atan (Vp/V)

Let us remember that near the center of the propeller, the relative speed is mainly composed of the speed V and that it is therefore substantially parallel to the propeller axise, and in that the blade tip speed is composed of the relative speed V + Vp and its direction is therefore more oriented towards the plane of rotation.

propeller's blades's twist compensates the variation of the apparent angle:

The elements of the blade are pieces of wings like the wings, they must receive fluid with a certain angle of incidences to create lift. To take into account the variation of the apparent wind, and for adjusting the element's angle of incidence to the optimum angle, the blade must be twisted. This change in the apparent velocity seen by the blade elements according to their position on the radius gives the reason for the twist of the propeller blades.

Warning: The speed actually received by the profile of the blade is slightly different from the apparent speed, because the profile acts on the direction and velocity of the fluid and induces a change:

The air just front of an airplane propeller that rotates while the aircraft is stopped, is drawn through the propeller !
The air just in front of a wind turbine turning is braked !

for example, if the apparent velocity is calculated by combining only the rotational speed and the fluid velocity far upstream of the plane stopped on the runway, we don 'have any axial component. Yet just front of the propeller, an axial air flow is indeed present and even dangerous because it draws us into the propeller! This flow of air current is induced by the propeller. It must be taken into account in calculating the twist to ensure that the incidence of the profile is properly assessed.

Calculation methods and theories will inform you on the induced velocity and its calculation. Of course, the software tool Heliciel calculating these speeds to create the optimum twist in your propeller and produce plans 3D to create the prototype.