Froude theory about turbines betz limit
Understand and master Froude theory on screew propeller, and wind turbines betz limit:
To understand Theory Froude, the notion of momentum must be mastered, because it is on the balance of momentum that the Froude theory is based ..
Froude method uses the equations of conservation of momentum to determine the performance of a propeller viewed as a uniformly loaded disc having an infinite number of blades. The axial induced velocities can thus beings evaluated
- we set the following assumptions, according to which:
- The rotation of the flow is neglected
- The fluid is incompressible
- The flow out of the duct through the disc is undisturbed
- The pressure at infinity upstream and downstream is equal to the static pressure
flow - Air passes through the rotor without friction
The continuity equation tells us that, to maintain a flow even if the speed decreases section must increase. If we observe the flow of the fluid stream passing through the disk, so we see the section increased by the braking of the fluid..Watch our propeller in a control volume larger than the vein through the propeller. We find that the expansion of vein can only be done if a certain amount of fluid is evacuated from the volume control..
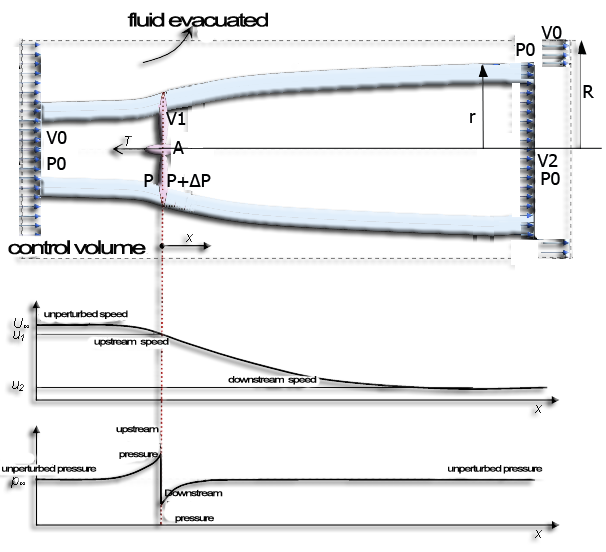
lthe continuity equation allows us to calculate the volume removed from the control zone per second (volume flow Q in m3/sec),
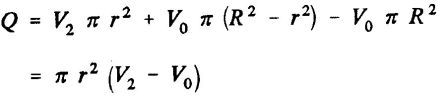
Q is the volumetric flow discharged from the volume control. From the theorem of momentum, the thrust, T of the propeller is obtained, that is to say the variation of the amount of movement between the sections 2 and O, whose projection on the horizontal axis indicates thrust :
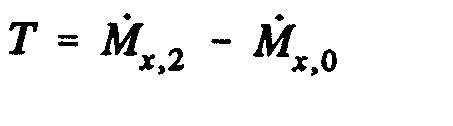
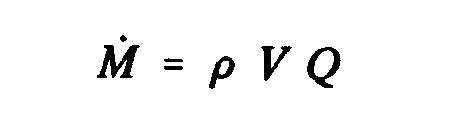
![]()
![]()

![]()
![]()
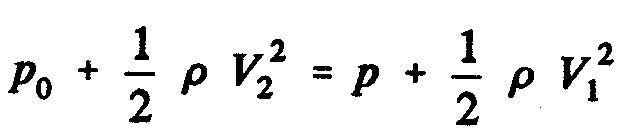
The static pressure difference between the upstream and downstream sides of the disk of the propeller as the expression:
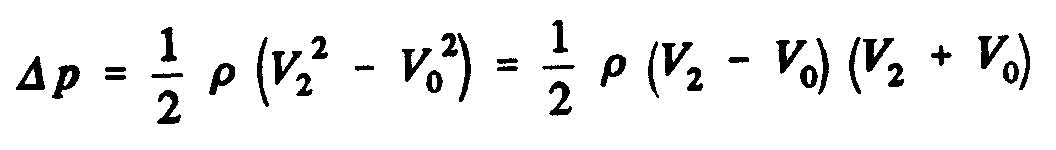
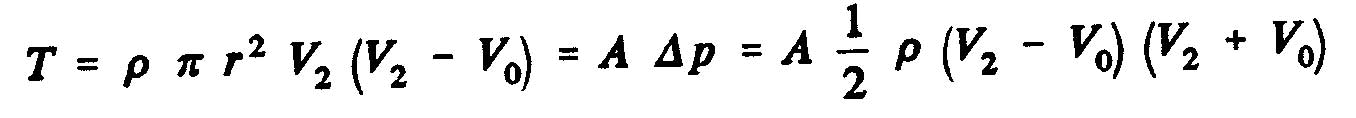
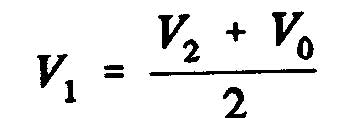
![]()
![]()
Now, if we consider the expression:
![]()
The power extracted from the wind :
![]()
The power coefficient is defined as the ratio between the available wind power and the power extracted:
![]()
Inserting the axial interference factor "a", defined as the fraction of the decrease in wind speed between the free-flow upstream of the rotor and the rotor plane :
- V=(1-a).V0
Using the equation:
- V1=(1-2a).V0
knowing:

substituent V and V1, is obtained :
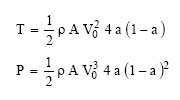
![]()
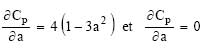
this gives :
![]()
The maximum efficiency for an ideal turbine is approximately 59.3%. In practice, this performance is never done because of the following effects :
- The air flow has a rotating component due to the rotation of the rotor.
- The drag force is never zero due to friction.
- The propeller contains a finite number of blades.
This simple one-dimensional model does not describe the rotating airflow, though it sets some basic concepts in the work of wind turbines.
So that the propeller extracts energy from the wind, the speed thereof must decrease when passing through the propeller. An ideal machine must slow down the wind speed of 2/3.
From the continuity equation (1), the section of the air swept by the wind increases from upstream to downstream. For an ideal wind turbine, the cross-sectional area of the flow upstream is 2/3 that of the rotor, and the latter is half that of the downstream section. Finally, the extraction of all available wind energy is virtually impossible, in practice, the performance of wind turbines does not exceed 45 %.
The theory froude gives us the axial induced velocity. It will be linked to the theory of the blade element to give a decomposition of the induced velocity in tangential and axial induced velocities necessary for the prediction of the incidence angles and the geometry of the blades..

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies