Blade element momentum theory: BEM for propeller
Understand and master BEM blade Element theory momentum about propeller:
Blade element momentum theory is a theory that combines both blade element theory and Froude momentum theory. The Theory of Froude , allowed us to do relation between lnduite axial velocity and thrust force. This theory, assumes that the flow undergoes no rotation, and does not give us indication shape to give our blade..
In reality, the law of conservation of angular momentum requires that the air must have a rotary motion, so that the rotor can extract an outputTorque. In this case, the direction of rotation of flow of the air is opposite to the rotor..Blade element momentum theory, builds on the results of the theory of froude to estimate the elementary axial force (relative to an element), and introduced performance profiles distributed by elements along the blade.The introduction of the rotational movement of air allows the model to better approximate the reality and get the induced velocities tangential and axial component brought by the theory froude using the variation of momentum induced velocity, thus more reliable results. The introduction of performance Cx and Cz profiles allows to determine the geometry and build a real blade.
The theory of the blade element, allows us to define an axial induction factor (a) and a tengentielle induction factor (a '). Solving a sytem equation iteratively converging introducing performance as Cx and Cz of the blade elements, it provides the induced velocities and therefore the performance of the elements.
In developing this model, the following assumptions are considered
- The upstream flow away from the plane of the rotor, is completely axial.
- In the plane of the rotor, the rotational angular velocity ω of the air is, the speed of the rotor reduces considerably far downstream, such that the static pressure far downstream can be considered equal to the atmospheric pressure.
- There is no interference between adjacent components of the blade.
- The flow of air around a part of the blade is considered to be bidimensional..
The method of Froude uses variations of momentum in a global volume control, here we use the ring elements as volume control, to know the change in amount of elemental movement, for each ring of the rotor. The sum of the performance of these rings give us the overall performance of the propeller..
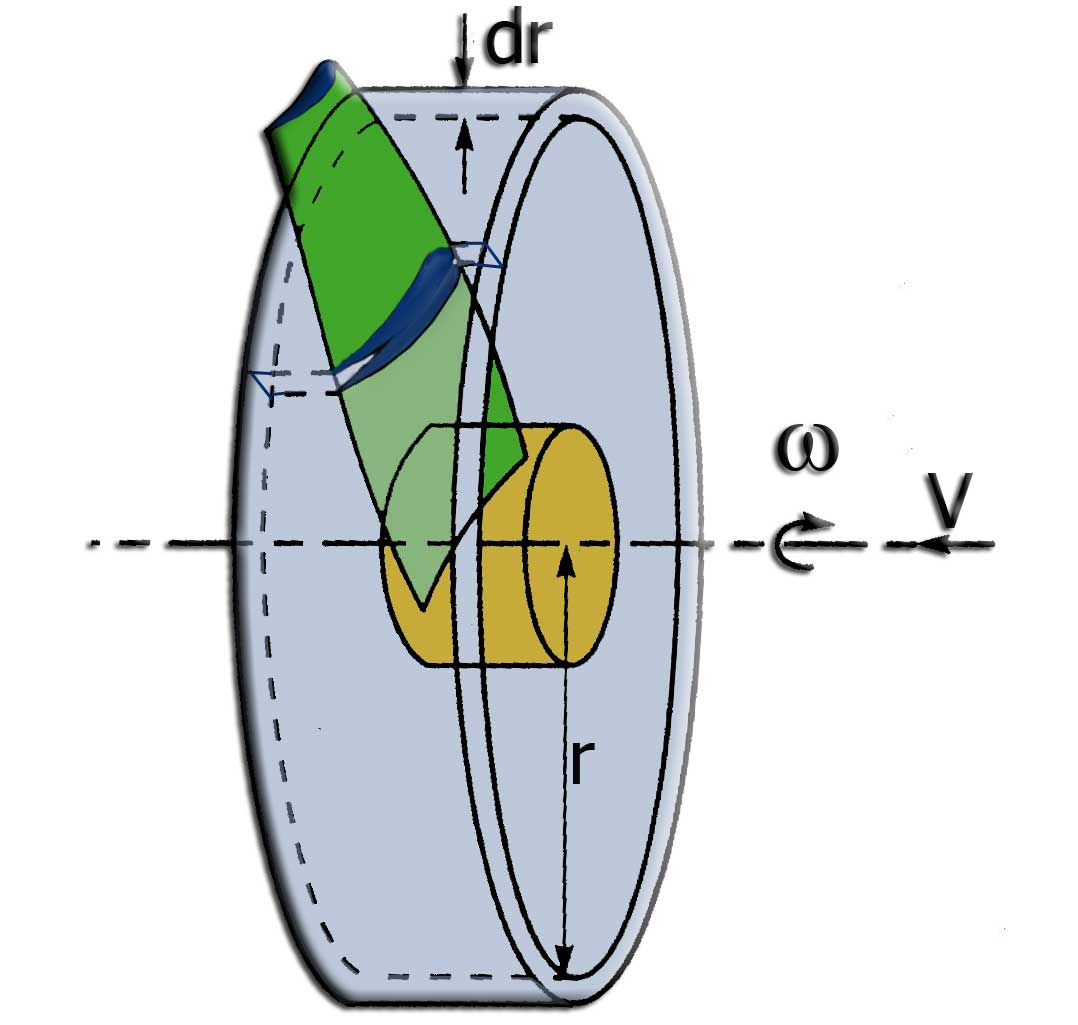
figure 1
Fig.1 shows the rotor rotating at an angular speed (a), moving at aspeed V, in the air A sectional view of part of a blade width dr, located at a
distance r from the axis of the rotor, is shown in Figure 2
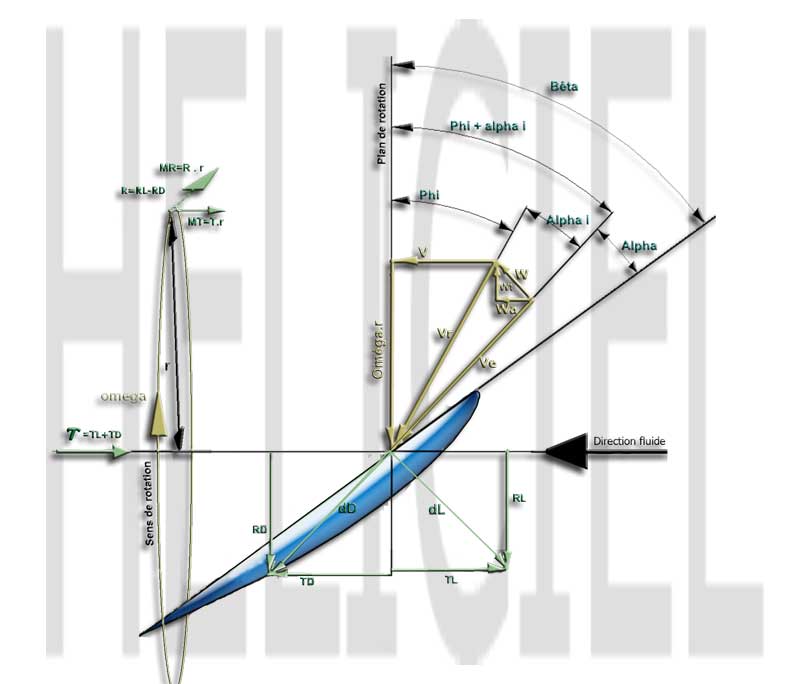
figure2
The figure illustrates the fact that the blade element is not subject to a flow, having a resultant speed, which depends only on the speed, and the rotational speed (Vr = V + wr), but a speed of "Ve" entry influenced by the induced velocities wt tangential, and axial wa.Using relations addition of forces along the axes in the plane of rotation and the axis of rotation of the rotor, it is possible to establish the equations of thrust and torque absorbed by an element of width dr, of a blade :
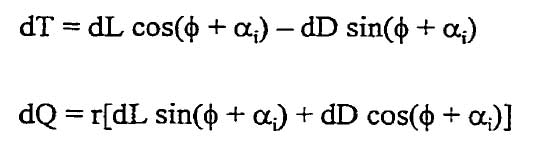
equ. 1 et 2
In these equations, and dD dL elements are forces acting on the profile, These forces can be calculated using the lift coefficient (CL), the coefficient of drag (Cd), chord (c) of the profile to the local radius (r) of the blade, thikness of annulus dr , p(rho) kg/m3
equ.3 et 4
the equation of thrust dT is used to evaluate the thrust developed by a circular ring of radius r, width (r) having a number of blades B. Combining equations 3 and 4 to the equation 1, the thrust on the circular ring gives: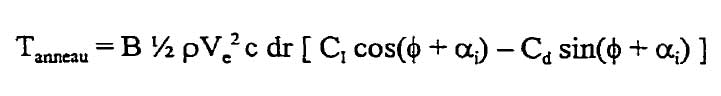

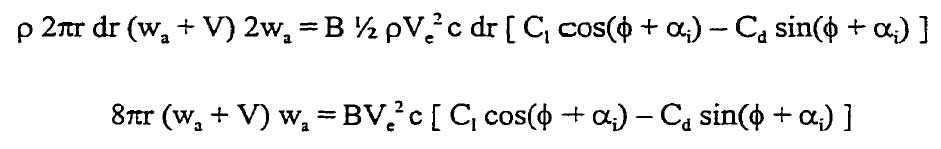
equ 6 et 7
whith: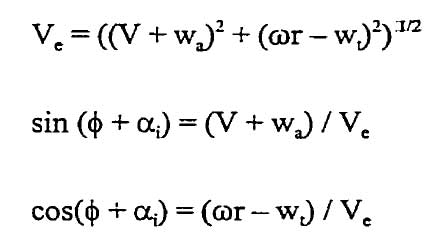
For more details: mémoire de mr Joncas

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies