L'evolution du calcul des helices nous apprend que chaque invention s'appuie sur l'observation mais aussi sur la connaissance des observations effectuées par nos prédécesseurs. Si " s'assoir sur les épaules du géant " signifie utiliser le savoir de nos pairs et pères, prenons donc un peu de hauteur , et de temps, pour lire ce résumé de l'evolution des methodes de calculs des hélices, un article sur l'histoire plus generale de l'helice et du calcul helice est aussi consultable.

 

Evolution modernes des methodes de calculs des hélices:

 

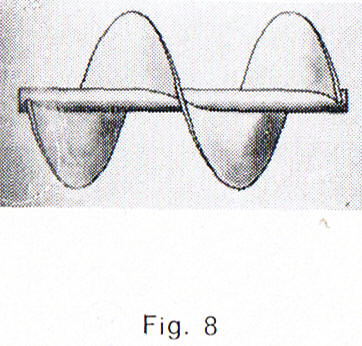
L’hélice, aux origines, était considérée comme une vis, progressant dans un milieu fluide exactement comme le fait la vis dans le bois ou le métal. Pour cette dernière, l’avance par tour est égale exactement au pas de la vis. On pensait que le rendement de l’hélice serait de 100/100 s’il en était ainsi pour elle, puisque l’avance selon l’axe serait égale pour chaque tour au pas de l’hélice. Ainsi en négligeant le frottement, le travail nécessaire pour faire tourner la vis correspond exactement  au travail nécessaire pour soulever un poids si nous prenons, par exemple, le cas d’un vérin. Il en est de même pour l’hélice (dans l’hypothèse où elle est assimilée à la vis) : le travail nécessaire pour faire tourner l’hélice (travail fourni par le moteur) correspond exactement au travail nécessaire pour " tirer "  l’avion, toujours au frottement près.

Mais en fait, pour l’hélice, il en va autrement:le fluide "cède" derrière l’hélice, ce qui fait que l’hélice « recule » par rapport à la position qu’elle occuperait si les fluides se comportaient comme les solides. Le rendement de l’hélice est donc inférieur à 1.

• le travail utile par tour étant le produit de la puissance de traction par l’avance réelle sur l’axe pour chaque tour d’hélice.

C’est ainsi que l’on peut exprimer ce qui en quelque sorte est la première théorie de l’hélice. Rankine alla plus avant. Il établit, en 1865, que l’action de l’hélice pouvait être essentiellement caractérisée par l’accélération de la masse d’air qui traverse cette hélice.

• D’où il découle que la variation de la quantité de mouvement dans l’unité de temps est égale à la poussée. Rankine établit également que l’accroissement de vitesse de la masse d’air produit par l’hélice doit être faible pour un bon rendement ; en d’autres termes il semblait qu’il y eût intérêt à augmenter indéfiniment le diamètre d’une hélice.Telle est la théorie de la « quantité de mouvement ». Elle permet de chiffrer un rendement idéal,puisqu’elle fournit la poussée ; mais elle n’explique rien sur le mode de transmission par lequel cette poussée passe de l’air à l’hélice.

Elle n’explique pas davantage le processus inverse : celui par lequel la puissance du moteur est transmise à l’air en passant par l’hélice.Rankine avait essayé par la suite de faire intervenir dans sa théorie la résistance de frottement des pales et l’interaction produite par des volumes proches de l’hélice. Mais c’est d’abord Froude, en 1889, qui l’a enrichie. Puis Betz la fait progresser encore en introduisant dans ses calculs la rotation du courant lié à l’hélice. Mais, même après ces améliorations, la théorie de la quantité de mouvement, si elle permet d’évaluer avec une grande précision traction et rendement, ne fournit aucune indication quant à la forme de pale correspondante.En 1878 Froude avait entrevu une autre voie dans la théorie de l’hélice, celle de « l’élément de pale fondée sur la connaissance des forces exercées par les pales dans leurs mouvements. Quelques années plus tard, Drzewiecki élaborait dans sa « Théorie Générale de l’Hélice »  la véritable théorie de l’élément de pale, que Froude n’avait fait qu’entrevoir : ici apparaissait la « géométrie « de la pale ; celle-ci était divisée en un grand nombre d’éléments, perpendiculairement au rayon, chacun d’eux étant considéré comme un profil avançant à une vitesse qui est la résultante de la vitesse d’avancement et de la vitesse tangentielle..

(extrait du livre l'hélice de jean GRAMPAIX édition Argenson paris 1966)

 

Voici l'avant propos de la "théorie générale de l'hélice"  publiée par S.Drzewiecki
en 1920 qui expose la  théorie de l’élément de pale :

.....Cette même théorie a aussi été étendue aux moulinets à air, et a permis de prévoir certains phénomènes nouveaux que l’expérience a confirmés. Je suis heureux d’être parvenu à mener à bonne fin le présent travail dont j’avais établi les premiers fondements il y a bien longtemps déjà, que j’ai développé depuis en maintes occasions et qu’il m’a été possible de parachever aujourd’hui grâce aux précieux renseignements expérimentaux qui m’ont été obligeamment fournis par le Laboratoire aérodynamique d’Auteuil où M. Eiffel, a bien voulu effectuer certains essais propres à éclairer la question. Je prie M. Eiffel de trouver ici l’expression de ma profonde gratitude. Toutefois, malgré les nombreux arguments, exposés ci-dessus, en faveur de cette théorie, il pouvait néanmoins subsister quelque doute au sujet de la légitimité de l’hypothèses  fondamentale qui lui servait de base, étant donné qu’aucune expérience directe et indispensable n’en avait encore établi le bien fondé. C’est pourquoi un certain nombre de savants, et non des moindres, tout en acceptant ces idées pour le détail de la question, persistaient encore à baser la théorie de l’hélice sur la conception de la masse fluide refoulée
par le propulseur, en admettant que cette masse refoulée, à la seconde, était celle d’un cylindre ayant pour base le cercle balayé par l’hélice et pour hauteur la vitesse de refoulement. Or, ces deux conceptions sont non seulement incompatibles entre elles, mais encore elles s’excluent mutuellement. En effet, si on admet, avec moi, que l'aile de l’hélice agit à l’instar d’une planchette exposée sous une certaine incidence dans un courant de fluide et qu’elle produit la déviation d’une certaine couche de fluide limitée, dont l’épaisseur dépend de la largeur de l’aile, de sa section, de son incidence, etc., il est bien évident que le flux ainsi engendré devrait se déplacer avec l’aile elle même, tout en restant parallèle à lui même, et constituer ainsi ce qu’on pourrait appeler un flux tournant à la vitesse de l’aile ; il devrait exister autant de ces flux qu’il y a d’ailes, et la perturbation entre les deux ailes devrait être moindre ou nulle. Si, au contraire. on admet la théorie opposée, le flux devrait être continu dans toute la section du cylindre, et les vitesses de refoulement devraient être constantes à la même distance de l'axe de rotation. Les mesures de vitesse effectuées jusqu’ici, en amont et en aval de l’hélice, semblaient confirmer cette dernière hypothèse ; mais ,si l’on examine la question de plus près, on comprend facilement la raison de cette contradiction apparente entre les résultats de ces essais et l’hypothèse fondamentale de ma théorie. Elle tient à ce que les anémomètres et les manomètres liquides qui servent à mesurer les pressions du tube de Pitot l'instruments dont on se sert exclusivement pour mesurer les vitesses des fluides, sont doués d’inertie et que, pour cette raison, ils ne sont pas en état de suivre les rapides changements de vitesses du fluide qui ont lieu au passage de chaque aile, et n’indiquent qu’un régime permanent, pour ainsi dire moyen, alors que le mouvement réel constitue une suite de pulsations qui se succèdent avec une grande rapidité. Pour élucider cette question délicate, il fallait pouvoir s’appuyer sur une expérience directe permettant de déterminer rigoureusement le mode d’écoulement du fluide lors du fonctionnement de l’hélice, et cela au moyen d’instruments de mesure dans lesquels l’influence de l’inertie aurait été écartée. II m’a été possible d’effectuer cette expérience avec un appareil que j’ai construit à cet effet et que j’ai pu expérimenter grâce à l’obligeance du Laboratoire Eiffel. Cette expérience a pleinement réussi et on en lira les détails dans le courant de ce travail ; elle a montré d’une façon irréfutable que le flux provoqué par le passage d’une aile d’hélice se déplaçait avec cette aile, ainsi que le faisait prévoir ma théorie, et que le fluide entre les deux ailes ne subissait que peu de perturbation. Aucun doute n’était dès lors possible ; la justesse de l’hypothèse qui sert de base à ma théorie était confirmée d’une façon directe et
irréfutable, tandis que l’hypothèse du flux cylindrique était du même coup réduite à néant. Le succès de cet essai décisif m’a encouragé à présenter au public cette étude sur les hélices.
S.Drzewiecki
 

Après la théorie de l’élément de pale, c’est, en 1912,la théorie tourbillonnaire de l’hélice propulsive de Joukowski.  Dans cette théorie, chaque pale de l’hélice est assimilée à un tourbillon attaché ou tourbillon pale dont la circulation est variable le long de la pale. Cette variation produit une nappe de tourbillons libres, issus de chaque élément de pale. Cette théorie, si l’on veut, est une combinaison des deux théories précédentes, quantité de mouvement et élément de pale. Elle a été perfectionnée par les travaux des Allemands Betz et Helmbold, de Karman, Biénen, des Anglais Wood et Glauert, de l’Italien Pistolési, de Lanchester, de Prandtl, des Japonais Moriya et Kawada

 

Voici l'introduction du "DEVELOPPEMENT MODERNE de la THEORIE DE L HELICE" de Raymond Siestrunck publié en 1947

 La théorie de l’hélice s’est constamment renouvelée et développée depuis l’apparition des premiers essais théoriques de Rankine (1865), à mesure que les connaissances sur le fonctionnement aérodynamique du propulseur et sur les surfaces portantes en général se furent approfondies ; les premières méthodes proposées traitent le problème d’une façon analogue à celui des turbines : l’hélice est constituée par une série d’éléments correspondant aux différentes sections de la pale et qu’on peut considérer comme sans interaction entre eux; le fluide arrive sur cet élément de pale avec une vitesse égale à la résultante des vitesses d’avancement et de rotation de l’élément, dont l’action est une déviation de l’écoulement du fluide, qu’on évalue par des considérations cinématiques; 0n en déduit, par application des théorèmes des quantités de mouvement et du moment cinétique, la poussée et le couple élémentaires fournis par l’élément, et les efforts totaux sont obtenus par intégration le long de
la pale. D’autres méthodes pénètrent un peu plus avant dans le mécanisme aérodynamique, en appliquant à chaque élément les lois théoriques ou expérimentales de la résistance des fluides, déterminées, bien entendu, sur des éléments en translation uniforme ; une intégration donne ensuite les expressions totales de traction et de couple ; ici, se placent les noms
de Redtenbacher (1875) et W. Froude (1878); on trouvera un exposé complet dans  la Théorie générale de l’hélice, Gauthier-Villars, 1920. de Drzewiecki . Sur une base assez différente se place alors la théorie connue de H.-E. Froude (1889), qui relie directement la poussée et la puissance motrice de l’hélice au sillage créé par celle-ci , l’analyse de ce sillage est incomplète puisqu’on admet que l’hélice communique au fluide qui la traverse une certaine vitesse de souffle uniformément répartie sur le disque qu’elle balaye, ou, ce qui revient au même, que l’effet de l’hélice est équivalent à une discontinuité de pression de part et d’autre de ce disque.Il faut attendre 1912 et les premiers mémoires de Joukovski  pour que la liaison s’effectue entre les théories précédentes; l’importance des émissions tourbillonnaires dans les échanges d’énergie est déjà démontrée, et la connaissance du sillage de l’hélice s’est beaucoup accrue depuis les expériences de Flamm (1909) ; c’est ce qui permet à Joukowski de jeter les bases de la théorie actuelle, dans laquelle on applique encore, à chaque élément de pale, les résultats expérimentaux des surfaces portantes, mais compte tenu de l’interaction des autres éléments, dont l’émission tourbillonnaire « induit » sur toute la pale des vitesses additionnelles. La liaison entre ces vitesses induites et le fonctionnement d’un élément est faite au moyen de la «circulation » qui caractérise la portance de chaque élément, par le théorème qui porte aujourd’hui le nom du savant russe. Les travaux de Joukowski n’avaient trait qu’à des hélices à distribution constante de la circulation le long de la pale, mais ils n’en devancent pas moins les travaux de l’école de Göttingen sur les surfaces portantes et les hélices (Prandtl et Betz) ; depuis lors, de nombreux travaux ont été publiés sur le problème de l’hélice, qui, à la mort de Joukowski, en I 92 I , était entièrement posé.

 L’élaboration ultérieure de la théorie tourbillonnaire de l’hélice, sur un modèle semblable à celui de Prandtl pour l’aile portante, s’est heurtée à des difficultés beaucoup plus grandes que n’en a eu cette dernière, et son développement a été, en conséquence, moins brillant et moins complet. Cela tient pour la plus grande part au fait que l’évaluation des vitesses additionnelles produites dans le sillage par les échappements tourbillonnaires ne peut être faite en termes simples dans le cas de l’hélice, et que, sauf dans quelques cas particuliers, les difficultés d’ordre mathématique paralysent le développement de la théorie. On a, néanmoins, mis au point des modes de solution approchée des différents problèmes concernant les hélices, soit qu’on s’attache à la détermination des caractéristiques de forme des propulseurs en vue de performances imposées, soit qu’on aborde le problème inverse, détermination des performances d’un propulseur donné et de la famille qu’on en déduit par variation continue du pas ; le premier point de vue a donné lieu, principalement, au travail connu de Goldstein (I929~, qui fournit, dans le champ de validité de la théorie, une solution rigoureuse du problème d’adaptation ; le deuxième point de vue conduit à des calculs qui sont d’un degré de complication nécessairement au moins égal à celui des méthodes employées pour les ailes (Glauert, Lotz), mais nous verrons qu’ils peuvent être rendus assez maniables pour permettre d’intéressantes confrontations entre la théorie et les mesures de soufflerie. Nous allons passer brièvement en revue les hypothèses qui sont à la base de la théorie actuelle de l’hélice, et signaler les principales difficultés qu’elles lèvent ou laissent subsister.....

Raymond Siestrunck 1947

le logiciel Heliciel utilise la methode de calcul d'helice par elements de pales couplée a la theorie de variation de quantité de moucement(Froude) integrant les pertes d'apres la théorie tourbillonnaire de l’hélice, avec les corrections de glauert ou Goldstein pour la prise en compte des cas de charges ou la theorie de froude n'est plus valide.